La Genèse des chiffres – 40 siècles pour créer le zéro

Thèmes : civilisation, histoire, société.
Conférence du mardi 3 mars 1994 par Jacques Thédié.

 

 

« Compter et calculer sont deux activités si familières qu’il nous semble volontiers que les chiffres font partie du patrimoine héréditaire de l’espèce humaine ».

« Et pourtant les chiffres sont une grande invention au même titre que le feu, la roue ou la charrue. Ils ne sont pas apparus d’un seul coup. Ils ont une origine et une histoire. Ils se sont peu à peu dégagés d’une profusion d’essais et de tâtonnements, de percées fulgurantes et de piétinements, voire régressions » – Georges lfrah.

De larges extraits de ce compte-rendu ont été tirés de l’ouvrage de Georges Ifrah – Histoire universelle des chiffres – Ed. Seghers.

 

***

 

De tous temps, nos doigts ont servi et servent parfois encore de support matériel au concept numérique.

L’adoption quasi universelle de la base 10 a été commandée par l’anatomie de nos mains, puisque c’est sur ses dix doigts que l’homme apprit à compter. Si nous avions eu six doigts à chaque main, notre numération serait fondée sur la base 12.

Certains peuples, comme les Celtes, les Mayas et les Aztèques ont pris très tôt l’habitude de compter sur la base 20 (10 doigts + dix orteils). Ainsi le calendrier comportait des mois de 20 jours, les cycles étaient de 20 ans, ils groupaient par vingtaines les êtres ou les objets qu’ils voulaient recenser.

Chez les Sumériens, le mode de numération est fondé sur la base 60. De nombreuses hypothèses ont été émises quant à cette utilisation, mais aucune ne paraît déterminante, parmi celles-ci :

• 60 est le plus commode à utiliser de tous les nombres, par le fait que, entre tous ceux qui ont le plus de diviseurs, étant le plus bas, il est le plus aisé à manier (Ptolémée),
• le nombre de jours de l’année, arrondi à 360, aurait donné la division du cercle en 360°, par le fait que la corde du sextant est égale au rayon, ce même nombre aurait engendré la division du cercle en six parties, ce qui aurait privilégié la soixantaine (le Vénitien Formaleoni),

 

Les méthodes de calcul

La main :

Plusieurs procédés particuliers de compte et de calcul sur les doigts ont été en honneur, dès la plus haute antiquité, chez une multitude de civilisations et ont parfois subsisté jusqu’à nos jours chez un certain nombre d’entre elles :

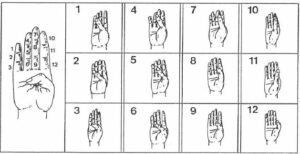
En Inde, en Indochine et en Chine méridionale, le calcul se pratique sur chacune des deux mains à l’aide d’un doigt de l’autre. Chaque phalange compte pour une unité, en commençant par la phalange inférieure du petit doigt pour finir par la phalange supérieure du pouce de la même main. Par cette technique on peut donc aller de 1 à 14 sur une main et jusqu’à 28 sur les deux. Les Musulmans emploient encore cette méthode lorsqu’ils n’ont pas de chapelet à leur disposition.

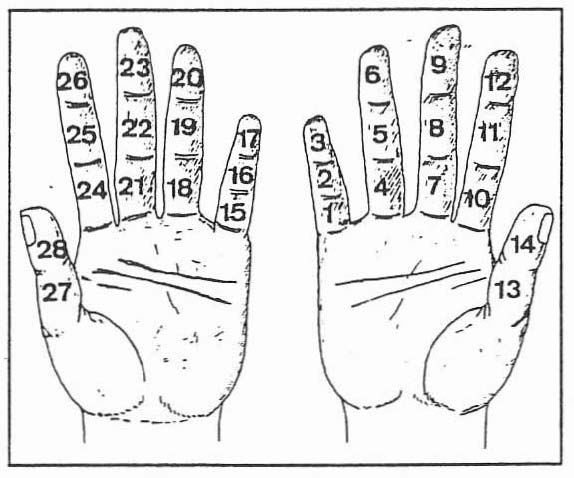
En Orient et Extrême-Orient, un autre système de calcul permet de compter sur une main une suite de 1 à 12. Il se pratique sur les phalanges des doigts d’une main, en s’aidant pour cela du pouce opposé. Cette technique permet de compter jusqu’à 12 (3 x 4), le pouce étant exclu du compte, et jusqu’à 24 avec les deux mains.

Ce système pourrait sans doute expliquer la tendance assez générale, au cours de l’histoire, à utiliser la douzaine en tant que base dans certaines divisions du temps, ainsi que dans certains comptes commerciaux (douzaine d’œufs, d’huitres…).

Des variantes de ce système digital permettent de compter jusqu’à 60 et même, chez les Chinois, jusqu’à 100 000 sur une seule main.

 

La pratique de l’entaille :

Les objets les plus anciens ayant servi de support au calcul sont probablement les os entaillés des hommes préhistoriques. Ces encoches constitueraient peut-être le témoignage d’une comptabilité du gibier abattu ou correspondraient aux différentes phases de la lune.

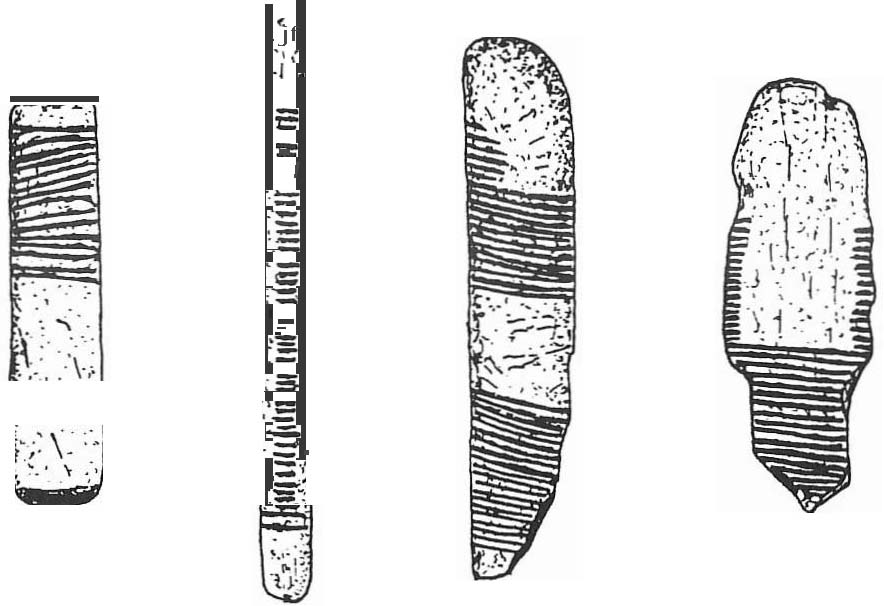
Cette méthode était employée en France, dans les boulangeries de campagne lorsqu’on y vendait du pain à crédit. Chaque fois qu’une miche de pain était vendue, une encoche était faite sur deux morceaux de bois appelés « tailles », dont l’un restait chez le boulanger et l’autre était remis au client.

La pratique de l’entaille en tant qu’instrument de compte crédit se retrouve à différentes époques et régions du monde.

 

Les cailloux :

Le mot « calcul » dérive du terme latin « calculus » qui signifie « petit caillou ». Cette méthode n’exige aucune mémoire, et ne demande aucune notion de nombre. Il suffit d’associer un caillou à une unité : le berger aura autant de cailloux que de moutons, 20 cailloux représenteront 20 guerriers, etc.

Mais cette méthode ne mène pas assez loin pour satisfaire les besoins sans cesse croissants de la vie quotidienne. Pour compter jusqu’à mille, il fallait amasser 1000 cailloux. On a donc utilisé des pierres de différentes tailles en leur attribuant un nombre différent.

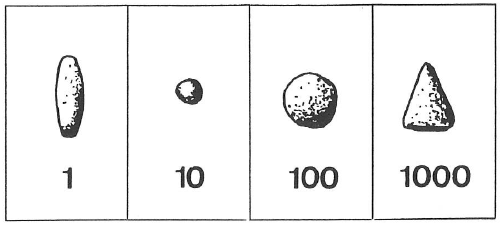
Devant la difficulté de trouver des cailloux de la même taille, on a perfectionné le système en donnant des formes différentes, par exemple un bâtonnet pour l’unité, une bille pour la dizaine, une sphère pour la centaine, un cône pour le millier.

 

Les ficelles :

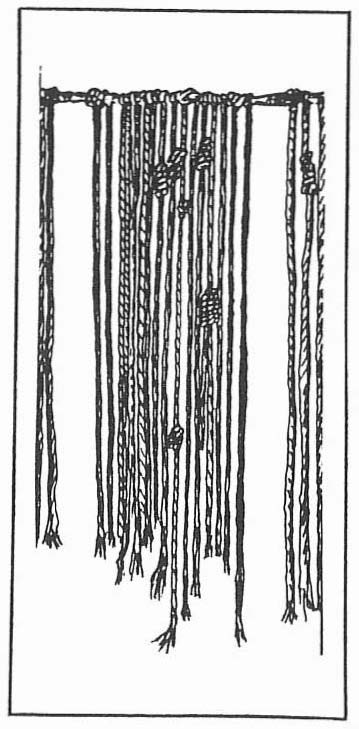
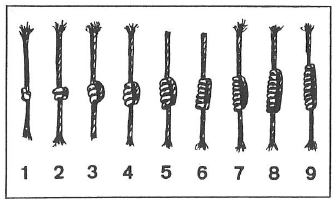
Les Incas utilisaient une cordelette à nœuds à laquelle étaient nouées des ficelles multicolores plus minces, rassemblées en plusieurs groupes et liées à intervalles réguliers par différentes espèces de nœuds.

Chaque couleur, chaque forme et position des nœuds avaient une signification numérique.

 

Les tables à calcul :

Les abaques :

Les plus courants étaient les tables à jetons qui consistaient en des tables ou des planchettes sur lesquelles des divisions en plusieurs lignes ou colonnes parallèles, tracées d’avance, séparaient les différents ordres d’unités. On y plaçait des petits cailloux ou des jetons. Chacune des colonnes parallèles symbolisait l’une des puissances successives de 10 (1, 10, 100, 1000, etc.).

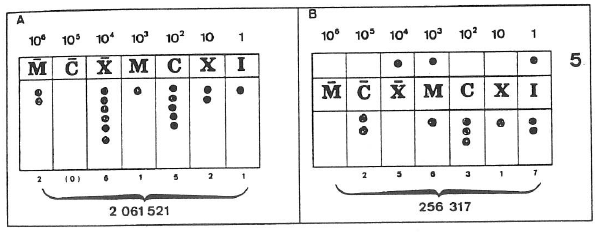
Les bouliers :

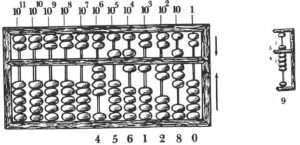
Le boulier chinois se présente sous forme d’un cadre rectangulaire de bois dur, composé d’un certain nombre de broches sur lesquelles sont enfilées sept boules mobiles qui peuvent s’éloigner ou se rapprocher d’une baguette transversale de telle manière que deux boules demeurent toujours au-dessus et cinq en-dessous.

La première broche à droite correspond aux dizaines, la seconde aux centaines, etc. Chacune des cinq boules inférieures a une valeur d’unité, et chacune de deux boules supérieures vaut cinq unités.

 

 

L’origine des chiffres

Les habitants de l’Inde avaient fait usage d’une numération écrite très rudimentaire où le chiffre n’évoquait plus visuellement le nombre correspondant. Par exemple, le chiffre 9 n’était pas composé de neuf barres ou de neuf points, il était représenté par un graphisme.

Les neuf premiers signes représentés ainsi allaient devenir, quelques siècles plus tard, ceux que nous appelons aujourd’hui (à tort) les chiffres arabes.

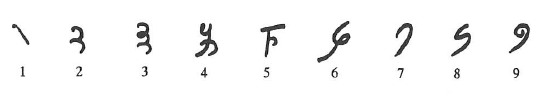
Dans cette numération, il était impossible d’aller au-delà de 99 999, ce qui ne pouvait satisfaire les besoins des savants indiens et plus spécialement les astronomes. Ils eurent donc l’idée d’exprimer les chiffres « en toutes lettres » ce qui devait les conduire à la découverte du principe de la position des nombres et du zéro :

 

. Position :

Cette numération orale attribuait un nom particulier à chacun des premiers nombres entiers, puis à la dizaine et à chacune de ses puissances, et des noms composés à tous les autres nombres.

Mais, au lieu de procéder comme nous, suivant les puissances décroissantes de dix, ils commençaient par les unités simples, et là où nous dirions « trois mille sept cent neuf », ils énonçaient en sanskrit « neuf, sept cent et trois mille », ce qui correspondait à neuf unités, sept centaines et trois milliers.

Mais la règle de position ne s’appliquait qu’à des mots et non pas aux chiffres. Ils utilisèrent une sorte d’abaque à colonnes et inscrivirent le nombre voulu :

. Zéro :

Par contre, la difficulté apparut pour exprimer, par exemple, 301, il fallait trouver un mot particulier pour signifier qu’il n’y avait pas de dizaine. Les savants firent appel à un mot « sunya » qui signifie « vide », on pouvait maintenant exprimer 301 par « un, vide, trois ». Ils venaient d’inventer le zéro.

Lorsqu’une unité manquait, il leur suffisait de laisser un vide :

Puis l’écriture des unités des différents ordres décimaux ne se fit plus dans le sens des puissances croissantes de dix, on représenta les nombres de gauche à droite, on symbolisa le zéro par un point ou, pour des raisons inconnues, par un petit rond :

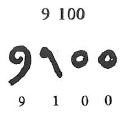
Les Indiens étaient parvenus, voici près de quinze siècles, à des techniques opératoires presque aussi simples et aussi rapides que celles d’aujourd’hui.

En concevant le zéro et en appliquant le principe de position à des chiffres de base, les Indiens franchirent les premiers pas conduisant à la numération écrite.

 

***

*

 

Les chiffres arabes

Au milieu du IXème siècle, les chiffres des Arabes ressemblaient à leurs modèles indiens, puis subirent des modifications graphiques pour s’adapter au style propre de l’écriture des pays arabes d’Orient :

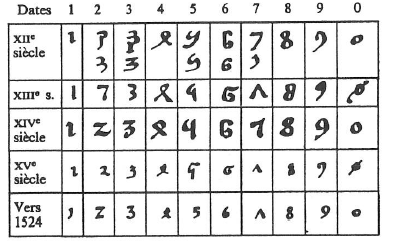
Au fil des siècles, les chiffres arabes évoluèrent et prirent peu à peu un aspect différent de la graphie hindie :

C’est cette graphie propre aux Arabes, qui, à partir de l’Espagne, atteindra les peuples chrétiens de l’Europe médiévale et qui, au XVIème siècle, sera celle que l’on connaît aujourd’hui.

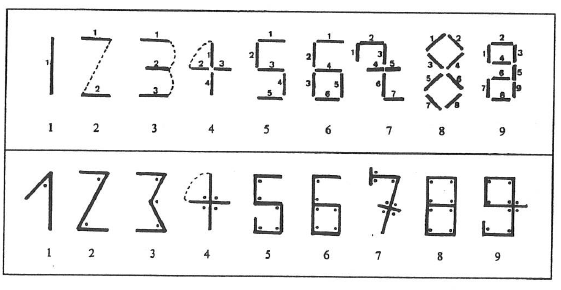
Les auteurs de la Renaissance avaient imaginé des moyens mnémotechniques pour faire retenir les graphismes de chiffres :

Notre système actuel : numération décimale de position, constitue une méthode parfaite qui permet de noter rationnellement n’importe quel nombre, si grand soit-il, en un minimum de signes.

Avec l’apparition des ordinateurs et des calculatrices électroniques de poche à cristaux liquides, on a cependant assisté à une évolution de la graphie des chiffres mais sans pourtant en modifier la structure.

 

***

*

 

Le zéro, cette invention difficile et géniale, et la découverte du principe de position ont créé l’arithmétique moderne et ouvert une ère totalement nouvelle dans l’histoire des mathématiques.

Ces découvertes sont anonymes, les noms des inventeurs sont perdus, sans doute à tout jamais, peut-être parce que ces inventions géniales ont été le fait d’hommes relativement humbles. L’inventeur du zéro, scribe méticuleux et soucieux de délimiter un emplacement dans une série de chiffres soumis au principe de position, n’a probablement jamais eu conscience de la révolution qu’il rendait possible.

 

 

Découvrez + de 1100 textes des conférences du CDI sur le site du CDI de Garches 

Vos commentaires et vos conseils contribuent à l’amélioration de nos parutions.
Vous disposez de l’espace « COMMENTAIRES » ci-dessous pour les exprimer.
Merci  et à bientôt pour votre prochaine visite.